来源:苏州环球教研中心
小编:曹姝妤 2135让美国高中生人人闻之色变的ACT数学,在中国学生看来却是小菜一碟,只要是个具有正常RP值,学过中国初高中数学课程的学生,看到ACT数学题目的那瞬间大多是心花怒放,因为我们甚至可以做到连题目都不看就可以选出正确答案。那为什么数学在美国学生眼中却显得那么恐怖呢?暑期学员Chris在美国华盛顿读教会中学,属于当地较好的中学了,他告诉我,在美国每次数学测试都是允许用计算机的,不仅如此,老师在考试的时候还会把考试过程中会用到的公理公式打印在纸上发给考生(WTF?!),而且老师出的题目也都是只要脑子正常应该都不会做错的那种,举个例子,比如一个直角三角形,告诉你两条边长让求第三边,然后老师会出四个选项,然而其中三个选项答案是负数……如此在温室里长大的美国中学生,看到ACT数学的时候,当然就惊叹了,为嘛五个答案都是正数这样他们怎么会做呢?!
言归正传,数学这一科目相比起其他四门而言对于中国学生的确是属于简单easy就能hold住的,但是很多考生在真正考试的时候也没法做到36分就拿全了,大多数考生是33-35,还有一些考生甚至只有30或30-。这其中一部分原因是ACT数学命题方向的改变,原先都是简单题型的数学题现在开始掺杂了一部分复杂的应用题,学生将会花更多的时间去看题结果竟然还看不懂题目,这就大大减小了学生做题的效率;第二个原因则是由于ACT数学考试本身内容涵盖量广,学生在复习的时候往往会漏掉那么一两个关键点,而考试又正好考到相关内容,从而导致了分数的流失。那如何在考前做好复习,应该复习哪些相关难点呢?今天就在此为大家进行简单的整理和归纳。
一、矩阵
矩阵属于线性代数范畴,但是其内容ACT考的并不难,但是矩阵这个概念只有普通高中的理科生才会接触到,所以对于大多数文科生以及外国语高中的学生来说,这是一个全新的知识点。但幸好,ACT数学在矩阵方面只考到3阶,平时老师上课的时候会说到4阶矩阵,所以只要上课认真听讲后这方面也不会有太大问题,而且ACT数学只考矩阵的加减乘,暂时没有遇到过除法运算,但是上课老师也讲过如果意外遇到除法该如何应对,所以考前复习矩阵是及其必要的。
矩阵的加减不多赘述,只是两个矩阵相对应位置数值的正常加减,而矩阵的乘法因为相对复杂,在下图中进行演绎:

还有一个需要多加说明就是矩阵的det值,ACT只考2×2矩阵的det值,所以只要进行ad-bc的运算就可以得出矩阵的det值。
二、复数
复数x被定义为二元有序实数对(a, b),记为z=a+bi,这里a和b是实数,i是虚数单位,如果虚部及bi等于0,则x为实数,如果实数a等于0,则x为纯虚数。ACT数学在复数部分主要涉及的是有关复数i2的四则运算,因为定义规定复数i2= -1,这边很多学生难以理解,平方是-1的话如何开根啊,所以我们要牢记i是虚数并不是实数。

上面这题就是非常典型的复数四则运算,其实只要按照多项式化出来,代入i2= -1,就可轻松获得正确答案J。

这题就是复数部分最难的一个题型了,首先因为已知其中一个根是2,所以可化得多项式(x-2)(2x2-5x+6),然后计算后面的二次方程就可获得另外两个答案,但是学生在做的时候发现△<0,在实数范畴内,当△<0则意味着方程无解,但是在虚数范畴下,我们仍可继续运算,△= -23就可看成△=23·i2,如此就可开根求解出正确答案J啦~~
三、三角函数
ACT数学中关于sin、cos、tan的计算主要集中在前30题,这个对于中国学生是没有任何难度的,但是偶尔会出现正割和余割,所以要花点心思记忆正割sec=1/cos,余割csc=1/sin。
数学后30题中则会以公式换算以及三角函数方程的形式出现,所以三角函数换算的一些公式学生在考试前还是要进行非常严谨的背诵,以此减少做题时推算公式所浪费的时间。
常考公式:
sin(A+B)=sinAcosB+cosAsinB
sin(A-B)=sinAcosB-sinBcosA
cos(A+B)=cosAcosB-sinAsinB
cos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB)
tan(A-B)=(tanA-tanB)/(1+tanAtanB)
sin2A=2sinA*cosA
cos2a=(cosa) 2-(sina)2=2(cosa)2-1=1-2(sina)2
tan2A=2tanA/[1-(tanA)2]
除此之外,三角函数方程图像也要牢记在心,函数递增递减的区域也要分别记忆,做好准备,考试的时候才能做到胸有成竹。
四、指数及对数
指数部分ACT数学考的不多,只要牢记两个公式解题时绝对不会遇到任何障碍难度的。
牢记公式:am*an=a(m+n)
am/an=a(m-n)
对数部分ACT就非常喜欢的不管是正着计算还是反着计算,总之是怎么烦就怎么出题,很多学生在做对数题的时候会因为找不到正确的切入点而浪费很多宝贵的时间,在此强调一点,不管是何种形式的对数题,其主要解题关键仍然是对数的四则运算公式,只要考前强行记忆一波,那任何位于高低难攻的对数题,都能迎刃而解啦。
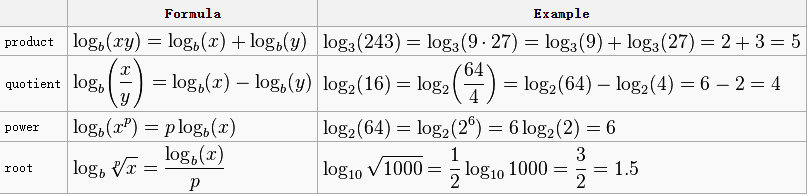
把上述四条内容在考前再次回顾复习一遍,带着满满的信心前往考场,相信每位考生都能获得ACT数学36分满分的佳绩!